第一章 单元测试
1、 问题:设事件A,B,C满足条件:P(AB)=P(AC)=P(BC)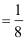 ,P(ABC)=
,P(ABC)=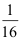 ,则事件A,B,C中至多一个发生的概率为。( )。
,则事件A,B,C中至多一个发生的概率为。( )。
选项:
A: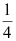
B: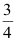
C: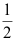
D: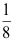
答案: 【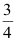
】
2、 问题:一射手对同一目标独立地进行4次射击,若至少命中一次的概率为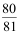 ,则该射手的命中率为 。( )。
,则该射手的命中率为 。( )。
选项:
A: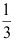
B: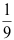
C: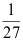
D: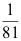
答案: 【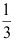
】
3、 问题:设两个相互独立的事件A和B都不发生的概率为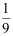 ,A发生B不发生的概率与B发生A不发生的概率相等,则P(A)=。( )
,A发生B不发生的概率与B发生A不发生的概率相等,则P(A)=。( )
选项:
A: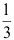
B: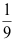
C: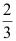
D: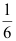
答案: 【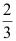
】
4、 问题:设一批产品中一、二、三等品各占60%、30%、10%,现从中任了一件,发现不是三等品,则取到的是一等品的概率为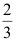 。( )
。( )
选项:
A:对
B:错
答案: 【
对
】
5、 问题:设A,B为随机事件且A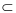 B,1>P(B)>0,则P(A)<P(A|B)成立。( )
B,1>P(B)>0,则P(A)<P(A|B)成立。( )
选项:
A:对
B:错
答案: 【
对
】
第二章 单元测试
1、 问题: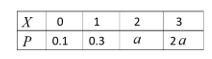 设随机变量X的分布律为则常数
设随机变量X的分布律为则常数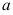 =( )。
=( )。
选项:
A:0.1
B:0.2
C:0.3
D:0.5
答案: 【
0.2
】
2、 问题:设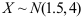 ,且
,且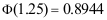 ,
,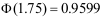 ,,则
,,则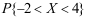 =( )。
=( )。
选项:
A:0.8543
B:0.1457
C:0.3541
D:0.2543
答案: 【
0.8543
】
3、 问题:设随机变量X的分布函数为: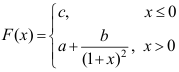 ,则下列正确的是( )。
,则下列正确的是( )。
选项:
A: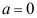
B: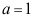
C: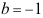
D: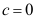
答案: 【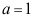
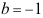
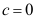
】
4、 问题:设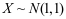 ,则
,则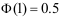 。( )
。( )
选项:
A:对
B:错
答案: 【
对
】
5、 问题:连续型随机变量的概率密度一定是连续函数。( )
选项:
A:对
B:错
答案: 【
错
】
第三章 单元测试
1、 问题:设二维随机变量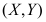 的概率密度为
的概率密度为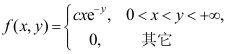 ,常数c=( )
,常数c=( )
选项:
A:0.5
B:1
C:1.5
D:3
答案: 【
1
】
2、 问题:设二维随机变量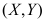 的概率密度为
的概率密度为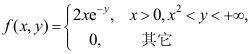 ,则随机变量X的边缘概率密度为( )
,则随机变量X的边缘概率密度为( )
选项:
A: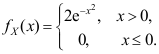
B: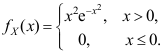
C: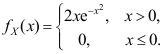
D: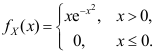
答案: 【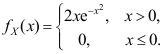
】
3、 问题:设两个随机变量X与Y相互独立,X在区间[0,2]服从均匀分布,Y服从参数为4的指数分布,则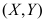 的联合概率密度为( )
的联合概率密度为( )
选项:
A: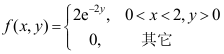
B: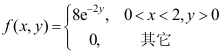
C: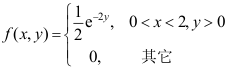
D: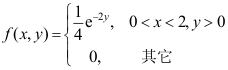
答案: 【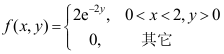
】
4、 问题:设两个随机变量X与Y相互独立且同分布: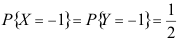 ,
,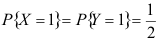 ,则
,则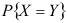 =( )
=( )
选项:
A:0.5
B:1
C:0.25
D:0.75
答案: 【
0.5
】
5、 问题:设二维随机变量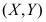 的概率密度为
的概率密度为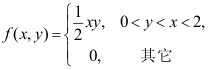 ,则
,则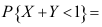 ( )
( )
选项:
A: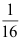
B: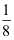
C: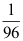
D: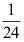
答案: 【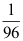
】
第四章 单元测试
1、 问题:某班工人每天生产中出现次品数X的概率分布为
则平均每天出次品( )件。
选项:
A:2
B:2.5
C:2.4
D:2.8
答案: 【
2.4
】
2、 问题:设连续型随机变量X的分布函数为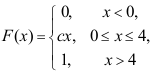 则X的方差为( ).
则X的方差为( ).
选项:
A: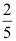
B: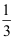
C: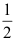
D: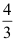
答案: 【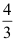
】
3、 问题:设随机变量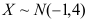 ,
,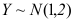 ,且X与Y相互独立,则
,且X与Y相互独立,则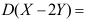 ( ).
( ).
选项:
A:12
B:8
C:6
D:3
答案: 【
12
】
4、 问题:设二维随机变量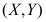 的概率密度为
的概率密度为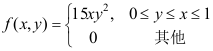 ,则
,则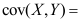 ( ).
( ).
选项:
A: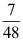
B:![]()
C: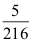
D: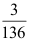
答案: 【![]()
】
5、 问题:设随机变量X具有密度函数 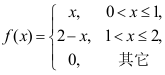 ,则
,则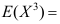 ( ).
( ).
选项:
A: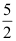
B: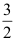
C: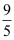
D: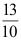
答案: 【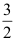
】
第五章 单元测试
1、 问题:测量某一物体的长度,我们一般用多次测量的算数平均值作为长度的近似值,解释这个现象的理论依据是( )。
选项:
A:切比雪夫大数定理
B:伯努利大数定理
C:辛钦大数定理
D:勾股定理
答案: 【
辛钦大数定理
】
2、
如无法购买,请复制网址,换浏览器打开
做题有答案,效率提高!使用过程中有疑问联系QQ55089918



还木有评论哦,快来抢沙发吧~