第一章 单元测试
1、 问题:下列关于效率的说法正确的是( )。
选项:
A:效率是一个性能要求,其目标应该在需求分析时给出
B:提高程序效率的根本途径在于选择良好的设计方法,数据结构与算法
C:效率主要指处理机时间和存储器容量两个方面
D:程序的效率与程序的长度强相关
答案: 【
效率是一个性能要求,其目标应该在需求分析时给出
提高程序效率的根本途径在于选择良好的设计方法,数据结构与算法
效率主要指处理机时间和存储器容量两个方面
】
2、 问题:算法的时间复杂度取决于( )。
选项:
A:问题的规模
B:待处理数据的初态
C:计算机性能
D:硬盘容量
答案: 【
问题的规模
待处理数据的初态
】
3、 问题:计算机算法指的是( )。
选项:
A:排序方法
B:解决问题的有限运算序列
C:计算方法
D:调度方法
答案: 【
解决问题的有限运算序列
】
4、 问题:归并排序法的时间复杂度和空间复杂度分别是( )。
选项:
A:O(n2)
B:O(nlog2n)
C:O(1)
D:O(n)
答案: 【
O(nlog2n)
O(n)
】
5、 问题:将长度分别为m,n的两个单链表合并为一个单链表的时间复杂度为O(m+n)。( )
选项:
A:对
B:错
答案: 【
错
】
6、 问题:用渐进表示法分析算法复杂度的增长趋势。( )
选项:
A:对
B:错
答案: 【
对
】
7、 问题:算法分析的两个主要方面是时间复杂度和空间复杂度的分析。( )
选项:
A:对
B:错
答案: 【
对
】
8、 问题:某算法所需时间由以下方程表示,求出该算法时间复杂度( )。
选项:
A:O(nlog2n)
B:O(n)
C:O(n2)
D:O(log2n)
答案: 【
O(nlog2n)
】
9、 问题:
下列代码的时间复杂度是( )。
选项:
A:O(1)
B:O(N)
C:O(log3N)
D:O(log2N)
答案: 【
O(log2N)
】
10、 问题:
下列算法为在数组A[0,…,n-1]中找出最大值和最小值的元素,其平均比较次数为( )。
选项:
A:3n/2
B: n-3/2
C:3n/2-3/2
D: 2n-1
答案: 【
3n/2-3/2
】
第二章 单元测试
1、 问题:可用Master方法求解的递归方程的形式为( )。
选项:
A:T(n)=aT(n/b)+f(n) , a≥1, b>1, 为整数, f(n)>0.
B:T(n)= T(n/a) +T(n/b) +f(n), a≥1, b>1
C:T(n)= T(n-a) +T(n-b) +f(n), a≥1, b>1
D:T(n)= T(n-a) +T(a) +f(n), a≥1
答案: 【
T(n)=aT(n/b)+f(n) , a≥1, b>1, 为整数, f(n)>0.
】
2、 问题:
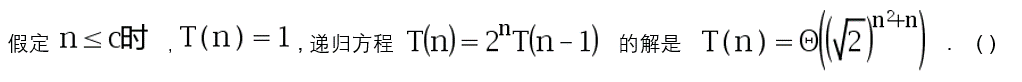
选项:
A:对
B:错
答案: 【
对
】
3、 问题:假定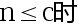 ,
,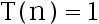 , 递归方程
, 递归方程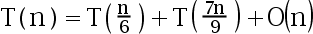 的解是
的解是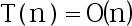 . ( )
. ( )
选项:
A:对
B:错
答案: 【
对
】
4、 问题:假设数组A包含n个不同的元素,需要从数组A中找出n/2个元素,要求所找的n/2个元素的中点元素也是数组A的中点元素。针对该问题的任何算法需要的时间复杂度的下限必为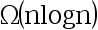 。 ( )
。 ( )
选项:
A:对
B:错
答案: 【
错
】
5、 问题:使用Master方法求解递归方程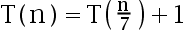 的解为( ).
的解为( ).
选项:
A: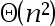
B: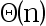
C: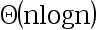
D: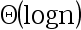
答案: 【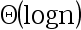
】
6、 问题:考虑包含n个二维坐标点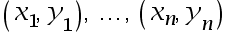 的集合S,其中n为偶数,且所有坐标点中的
的集合S,其中n为偶数,且所有坐标点中的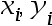 均不相同。一条竖直的直线若能把S集合分成左右两部分坐标点个数相同的子集合,则称直线L为集合S的一条分界线。若给定集合S,则可在
均不相同。一条竖直的直线若能把S集合分成左右两部分坐标点个数相同的子集合,则称直线L为集合S的一条分界线。若给定集合S,则可在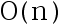 时间内找到这条分界线L。 ( )
时间内找到这条分界线L。 ( )
选项:
A:对
B:错
答案: 【
对
】
7、 问题:
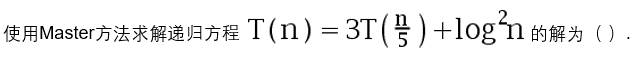
选项:
A: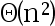
B: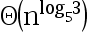
C: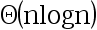
D: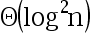
答案: 【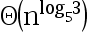
】
8、 问题:从n个数中找出前k个最小的元素并对所选择的前k个最小的元素进行排序。使用归并排序算法将这n个数进行排序的时间复杂度为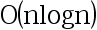 ,从排好序的数组中提取有序的k个最小数的时间复杂度为
,从排好序的数组中提取有序的k个最小数的时间复杂度为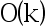 ,因此总的运行时间复杂度为
,因此总的运行时间复杂度为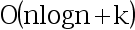 . ( )
. ( )
选项:
A:对
B:错
答案: 【
对
】
9、 问题:假定问题对于规模为n的所有不同输入,存在一个分治算法其平均时间复杂度为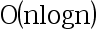 ,则算法在最坏情形下的时间复杂度可能为
,则算法在最坏情形下的时间复杂度可能为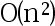 ( )
( )
选项:
A:对
B:错
答案: 【
对
】
10、 问题:使用分治算法求解最大最小问题。假定问题的规模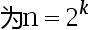 , 每次将问题分成规模接近的两个子问题,递归地对子问题求解并将子问题的解合并得到大问题的解,该分治算法的复杂度函数可写为 ( )
, 每次将问题分成规模接近的两个子问题,递归地对子问题求解并将子问题的解合并得到大问题的解,该分治算法的复杂度函数可写为 ( )
选项:
A: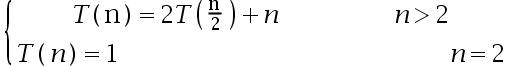 ,
,
B: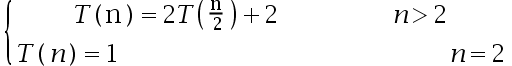
C: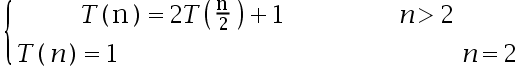
D: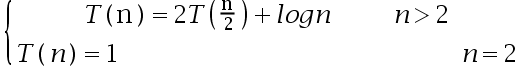
答案: 【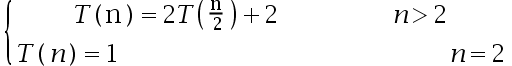
】
第三章 单元测试
1、 问题:在一个至少包含三个顶点的加权连通单向图中,假定边的权重互不相同,则权重最大的边不可能被包含在任何最小生成树中。 ( )
选项:
A:对
B:错
答案: 【
错
】
2、 问题:令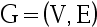 是一个加权图,令T是G的最小生成树,则T中任意两个顶点
是一个加权图,令T是G的最小生成树,则T中任意两个顶点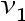 和
和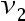 之间的路径必定是图G中该两点之间的最短路径。 ( )
之间的路径必定是图G中该两点之间的最短路径。 ( )
选项:
A:对
B:错
答案: 【
错
】
3、 问题:对于一个加权连通无向图,在Kruskal’s MST (KrusKal’s最小生成树)算法中, 若使用最大队列代替最小队列,则可生成一个最大成本树(而不是最小成本树). ( )
选项:
A:对
B:错
答案: 【
对
】
4、 问题:贪心算法适用于求解的问题一般具备以下几个特征 ( ) .
选项:
A:满足贪心选择性质
B:问题可分为相互独立的子问题
C:满足最优子结构性质
D:子问题的解相互独立
答案: 【
满足贪心选择性质
满足最优子结构性质
】
5、 问题:0/1背包问题是NP-hard问题,任何求解0/1背包问题的贪心算法都不能保证得到该问题的最优解。 ( )
选项:
A:对
B:错
答案: 【
对
】
6、 问题:一个连通图中具有最小权重的边,必定被包含在图的最小生成树中。 ( )
选项:
A:对
B:错
答案: 【
对
】
7、 问题:一个问题的贪心选择性质是指问题的最优解可通过一系列具备最优(贪心)选择得到。 ( )
选项:
A:对
B:错
答案: 【
对
】
8、 问题:贪心算法所做出的选择可能依赖于到目前为止已经做出的选择,但是不依赖于将来的选择或子问题的解。 ( )
选项:
A:对
B:错
答案: 【
对
】
9、 问题:贪心算法是一种自顶向下的求解方法,分步做出贪心选择,逐步将问题变成规模较小的问题求解。 ( )
选项:
A:对
B:错
答案: 【
对
】
10、 问题:下列问题可使用贪心算法求得最优解的是( ).
选项:
A:货箱装载问题
B:0/1背包问题
C:偶图覆盖问题
D:集合覆盖问题
答案: 【
货箱装载问题
】
第四章 单元测试
1、 问题:动态规划的适用条件为( )。
选项:
A:无后效性
B:子问题的重叠性
C:子问题相互独立
D:最优子结构性质
答案: 【
无后效性
子问题的重叠性
最优子结构性质
】
2、 问题:(1)计算动态规划
如无法购买,请复制网址,换浏览器打开
做题有答案,效率提高!使用过程中有疑问联系QQ55089918



还木有评论哦,快来抢沙发吧~