第一章 单元测试
1、 问题:如果函数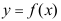 的定义域是[0,1],则函数
的定义域是[0,1],则函数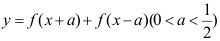 的定义域为( )。
的定义域为( )。
选项:
A:[a-1, a+1];
B:[a, -a+1];
C:[a-1, 1-a];
D:[1-a, a-1].
答案: 【
[a, -a+1];
】
2、 问题:下列数列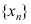 中,收敛的是( )。
中,收敛的是( )。
选项:
A: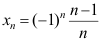 ;
;
B: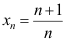 ;
;
C: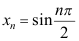 ;
;
D: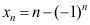 .
.
答案: 【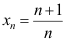 ;
;
】
3、 问题:设数列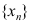 ,当
,当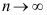 时的极限为a,则下列说法错误的是( )。
时的极限为a,则下列说法错误的是( )。
选项:
A:去掉数列的前1000项后,余下的数列还有极限,但极限不一定是a;
B:如果去掉所有的偶数项,只留奇数项,余下的数列还有极限,且极限仍是a;
C: ;
;
D: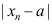 的值随着n的无限增大而无限减小.
的值随着n的无限增大而无限减小.
答案: 【
去掉数列的前1000项后,余下的数列还有极限,但极限不一定是a;
】
4、 问题:当n无限增大时,数列xn以常量A为极限,则xn与A之差是( )。
选项:
A:预先给定的任意小的正数;
B:任意小的正数;
C:无穷小量;
D:常量.
答案: 【
无穷小量;
】
5、 问题: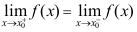 是
是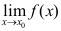 存在的( )。
存在的( )。
选项:
A:充分条件,但不是必要条件;
B:必要条件,但不是 充分条件;
C:充分必要条件;
D:既不是充分条件也不是必要条件.
答案: 【
充分必要条件;
】
6、 问题:两个无穷小量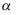 与
与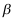 之积
之积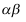 仍是无穷小量,且与
仍是无穷小量,且与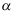 或
或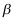 相比( ).
相比( ).
选项:
A:是高阶无穷小;
B:是同阶无穷小;
C:可能是高阶无穷小,也可能是同阶无穷小 ;
D:与阶数较高的那个同阶.
答案: 【
是高阶无穷小;
】
7、 问题:下列命题正确的是( ).
选项:
A:两无穷大之和为无穷大;
B:两无穷小之商为无穷小;
C: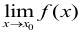 存在当且仅当
存在当且仅当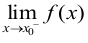 与
与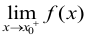 均存在;
均存在;
D: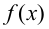 在点
在点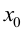 连续当且仅当它在点
连续当且仅当它在点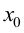 既左连续又右连续.
既左连续又右连续.
答案: 【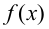 在点
在点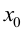 连续当且仅当它在点
连续当且仅当它在点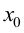 既左连续又右连续.
既左连续又右连续.
】
8、 问题:若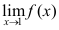 存在,且
存在,且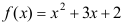
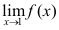 ,则
,则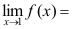 ( ).
( ).
选项:
A: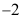 ;
;
B: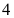 ;
;
C: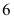 ;
;
D: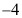 .
.
答案: 【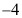 .
.
】
9、 问题: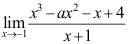 具有极限
具有极限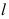 ,则下列说法正确的是( ).
,则下列说法正确的是( ).
选项:
A: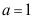 ;
;
B: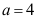 ;
;
C: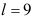 ;
;
D: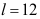 .
.
答案: 【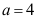 ;
;
】
10、 问题:已知极限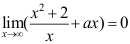 ,则常数
,则常数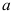 等于( ).
等于( ).
选项:
A:-1;
B:0;
C:1;
D:2.
答案: 【
-1;
】
11、 问题:下列命题正确的是( ).
选项:
A:无穷小量的倒数是无穷大量;
B:无穷小量是以零为极限的变量;
C:无穷小量是绝对值很小很小的数;
D:无界变量一定是无穷大量.
答案: 【
无穷小量是以零为极限的变量;
】
12、 问题: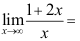 ( ).
( ).
选项:
A:0;
B:1;
C:2;
D: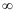 .
.
答案: 【
2;
】
13、 问题:下列等式成立的是( ).
选项:
A: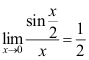 ;
;
B: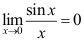 ;
;
C: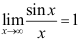 ;
;
D: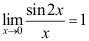 .
.
答案: 【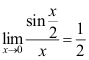 ;
;
】
14、 问题:下列极限计算正确的是( ).
选项:
A: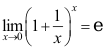 ;
;
B: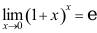 ;
;
C: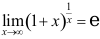 ;
;
D: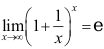 .
.
答案: 【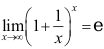 .
.
】
15、 问题:若函数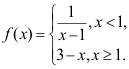 ,则
,则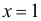 是函数
是函数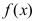 的( ).
的( ).
选项:
A:连续点;
B:可去间断点;
C:跳跃间断点;
D:无穷间断点.
答案: 【
无穷间断点.
】
第二章 单元测试
1、 问题:如果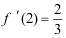 ,则
,则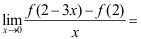 ( )。
( )。
选项:
A:-3
B:-2
C:2
D:3
答案: 【
-2
】
2、 问题:曲线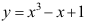 在点(1,1)处的切线方程为( )。
在点(1,1)处的切线方程为( )。
选项:
A: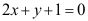
B: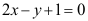
C: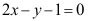
D: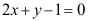
答案: 【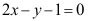
】
3、 问题:如果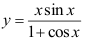 ,则
,则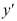 = ( ).
= ( ).
选项:
A: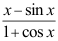
B: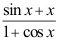
C: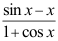
D: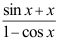
答案: 【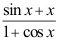
】
4、 问题:如果函数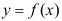 在点
在点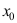 处可微,则下列结论中不正确的是( )。
处可微,则下列结论中不正确的是( )。
选项:
A:极限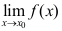 不存在
不存在
B: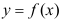 在点
在点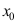 处连续
处连续
C: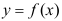 在点
在点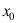 处可导
处可导
D: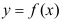 在点
在点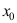 处有定义
处有定义
答案: 【
极限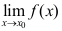 不存在
不存在
】
5、 问题:如果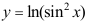 ,则
,则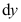 = ( ).
= ( ).
选项:
A: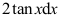
B: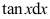
C: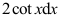
D: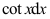
答案: 【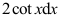
】
6、 问题:如果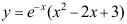 ,则
,则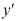 = ( ).
= ( ).
选项:
A: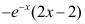
B: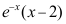
C: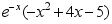
D: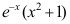
答案: 【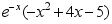
】
7、 问题:设函数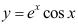 ,则
,则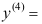 ( ).
( ).
选项:
A: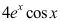 ;
;
B: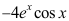 ;
;
C: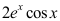 ;
;
D: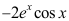 .
.
答案: 【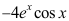 ;
;
】
8、 问题:由方程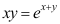 所确定的隐函数
所确定的隐函数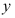 的导数
的导数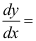 ( ).
( ).
选项:
A: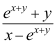 ;
;
B: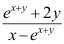 ;
;
C: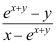 ;
;
D: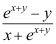 .
.
答案: 【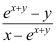 ;
;
】
9、 问题:设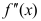 存在,那么
存在,那么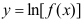 的二阶导数等于( ).
的二阶导数等于( ).
选项:
A: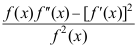 ;
;
B: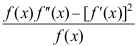 ;
;
C: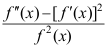 ;
;
D: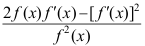 .
.
答案: 【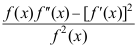 &n
&n
如无法购买,请复制网址,换浏览器打开
做题有答案,效率提高!使用过程中有疑问联系QQ55089918



还木有评论哦,快来抢沙发吧~