绪论 单元测试
1、 问题:
经典控制理论以单变量线性定常系统作为主要的研究对象，以时域法作为研究控制系统动态特性的主要方法。
选项：
A:错
B:对
答案: 【错】
2、 问题:
1892年俄国数学家李亚普诺夫发表了论文《运动稳定性的一般问题》，用严格的数学分析方法全面地论述了稳定性问题。
选项：
A:错
B:对
答案: 【对】
3、 问题:
现代控制理论以多变量线性系统和非线性系统作为研究对象，以时域法，特别是状态空间方法作为主要的研究方法。
选项：
A:错
B:对
答案: 【对】
4、 问题:
研究系统控制的一个首要前提是建立系统的数学模型，线性系统的数学模型主要有两种形式，即时间域模型和频率域模型。
选项：
A:对
B:错
答案: 【对】
5、 问题:
下述描述中哪些作为现代控制理论形成的标志（ ）。
选项：
A:最优控制中的Pontriagin极大值原理和Bellman动态规划
B:随机系统理论中的Kalman滤波技术
C:最优控制理论的产生
D:用于系统的整个描述、分析和设计过程的状态空间方法
答案: 【最优控制中的Pontriagin极大值原理和Bellman动态规划;
随机系统理论中的Kalman滤波技术;
用于系统的整个描述、分析和设计过程的状态空间方法】
第一章 单元测试
1、 问题:
输入输出描述是描述系统输入变量和输出变量关系的模型。
选项：
A:错
B:对
答案: 【对】
2、 问题:
状态空间描述能完全表征系统的一切动力学特征。
选项：
A:错
B:对
答案: 【对】
3、 问题:
系统的状态是指能够完全表征系统时间域行为的一个最小内部变量组。
选项：
A:错
B:对
答案: 【对】
4、 问题:
系统的状态空间描述是唯一的。
选项：
A:对
B:错
答案: 【错】
5、 问题:
坐标变换是指将系统在状态空间的一个基底上的表征，化为另一个基底上的表征。
选项：
A:对
B:错
答案: 【对】
6、 问题:
当状态空间描述中的A矩阵有相同的特征值时，一定不能将其化成对角规范形。
选项：
A:对
B:错
答案: 【错】
7、 问题:
并联组合系统的传递函数矩阵为各并联子系统的传递函数矩阵之和。
选项：
A:错
B:对
答案: 【对】
8、 问题:
若两个子系统输出向量的维数相同，则可实现反馈连接。
选项：
A:错
B:对
答案: 【错】
9、 问题:
线性定常系统线性非奇异变换后（ ）。
选项：
A:系统的传递函数矩阵改变
B:系统的特征值不变
C:状态空间描述各参数矩阵不变
D:系统的稳定性可能改变
答案: 【系统的特征值不变】
10、 问题:
考虑如图所示的串联组合系统，下列论述正确的是（ ）。
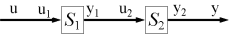
选项：
A:若两个子系统均为既能控又能观，则串联组合系统一定也是既能控又能观的
B:串联组合后系统的传递函数矩阵为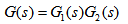
C:当子系统输入向量的维数与子系统输入向量的维数相同时，二者才可以进行串联
D:串联组合后系统的状态方程为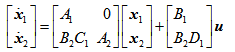
答案: 【串联组合后系统的状态方程为】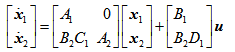
第二章 单元测试
1、 问题:
一般线性系统状态方程的解由两部分组成，第一部分反映系统初态的影响，第二部分反映系统输入对状态的影响。
选项：
A:对
B:错
答案: 【对】
2、 问题:
零初态响应指系统初始状态为零时，由系统输入单独作用所引起的运动。
选项：
A:错
B:对
答案: 【对】
3、 问题:
零输入响应代表系统状态的自由运动，受外部输入变量的影响。
选项：
A:对
B:错
答案: 【错】
4、 问题:
线性定常系统和线性时变系统的状态转移矩阵均为系统的矩阵指数函数。
选项：
A:错
B:对
答案: 【错】
5、 问题:
系统的状态转移矩阵由系统矩阵A唯一地确定。
选项：
A:对
B:错
答案: 【对】
6、 问题:
当且仅当状态方程的解为存在和唯一，对系统的运动分析才有意义。
选项：
A:错
B:对
答案: 【对】
7、 问题:
已知系统的初始状态和矩阵指数函数如下所示，
，
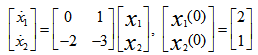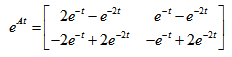
则其初始状态激励的响应为 ( )。
选项：
A: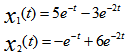
B: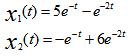
C: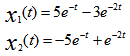
D: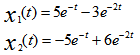
答案: 【】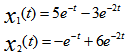
8、 问题:
已知系统的初始状态和矩阵指数函数如下所示
，
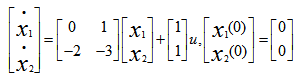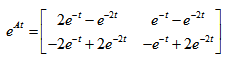
则输入u(t)=1激励的响应为 ( )。
选项：
A: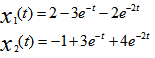
B: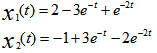
C: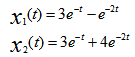
D: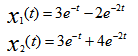
答案: 【】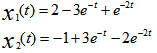
9、 问题:
已知系统的状态转移矩阵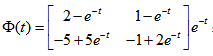
，则它的逆矩阵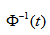为
为（ ）。
选项：
A: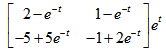
B: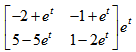
C: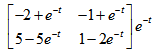
D: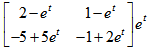
答案: 【】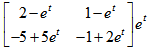
10、 问题:
已知系统状态转移矩阵为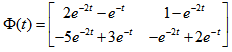
，则A矩阵为（ ）。
选项：
A: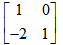
B: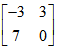
C: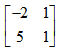
D: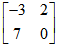
答案: 【】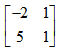
第三章 单元测试
1、 问题:
格拉姆矩阵能控性判据因计算简单，适用于高维系统的能控性判别。
选项：
A:错
B:对
答案: 【错】
2、 问题:
所有具有对角规范形描述形式的系统都可用对角规范形能控性判据判别其能控性。
选项：
A:对
B:错
答案: 【错】
3、 问题:
能控性和能观测性是从控制和观测角度表征系统机构的两个基本特性。
选项：
A:错
B:对
答案: 【对】
4、 问题:
能控性秩判据是基于系数矩阵A和C判断系统能观测性的一类判据。
选项：
A:错
B:对
答案: 【错】
5、 问题:
构造多输入多输出系统能控规范形和能观测规范形，都需要面临一个共性的问题，即找出能控性判别矩阵中n个线性无关列或能观测判别矩阵中n个线性无关行。
选项：
A:对
B:错
答案: 【对】
6、 问题:
对于下列状态空间描述及其所描述的系统说法正确的是（ ）。
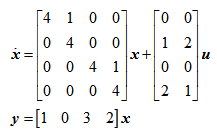
选项：
A:该状态空间描述为能控规范形描述
B:该状态空间描述为对角规范形描述
C:描述的系统为完全能控的系统
D:该状态空间描述为约当规范形描述
答案: 【描述的系统为完全能控的系统;
该状态空间描述为约当规范形描述】
7、 问题:
关于下列系统描述正确的为（ ）。
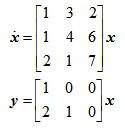
选项：
A:该系统的不完全能观测但完全能控
B:该系统的能控性无法判断
C:该系统完全能观测
D:该系统不完全能观测
答案: 【该系统完全能观测】
8、 问题:
能使下列系统完全能控的待定参数a,b,c的正确取值范围是（ ）。
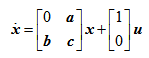
选项：
A:a=任意有限值，b≠0，c≠0
B:a=任意有限值，b≠0，c=任意有限值
C:a=任意有限值，b=任意有限值，c=任意有限值
D:a=任意有限值，b=任意有限值，c≠0
答案: 【a=任意有限值，b≠0，c=任意有限值】
9、 问题:
下列说法正确的是（ ）。
选项：
A:系统可由传递函数矩阵完全表征，当且仅当系统为完全能控和完全能观测
B:按能控性的系统结构分解的途径是引入基于不完全控性特征的特定线性非奇异变换
C:系统结构分解的结果唯一，形式不唯一
D:系统为完全能控和完全能观测时其传递函数矩阵不可简约
答案: 【系统可由传递函数矩阵完全表征，当且仅当系统为完全能控和完全能观测;
按能控性的系统结构分解的途径是引入基于不完全控性特征的特定线性非奇异变换;
系统为完全能控和完全能观测时其传递函数矩阵不可简约】
10、 问题:
关于下列系统说法正确的是( )。
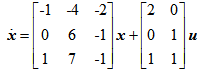
选项：
A:该系统的能控性指数为1
B:该系统的能控性指数为2
C:该系统的能控性指数集为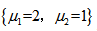
D:该系统的能控性指数集为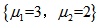
答案: 【该系统的能控性指数为2;
该系统的能控性指数集为】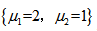
第四章 单元测试
1、 问题:
外部稳定性，是通过零输入下的状态运动响应来描述系统的稳定性。
选项：
A:对
B:错
答案: 【错】
2、 问题:
系统的内部稳定性和外部稳定性是等价。
选项：
A:对
B:错
答案: 【错】
3、 问题:
系统的内部稳定性和外部稳定性在任何情况下都不等价。
选项：
A:错
B:对
如无法购买，请复制网址，换浏览器打开 使用过程中有疑问联系QQ55089918
发布评论 （0条评论）
还木有评论哦，快来抢沙发吧~